domingo, 11 de diciembre de 2011
Teorema del valor medio
Sea f es una función continua en [a, b] y derivable en (a, b), existe un punto c  (a, b) tal que:
(a, b) tal que:

La interpretación geométrica del teorema del valor medio nos dice que hay un punto en el que la tangente es paralela a la secante.
El teorema de Rolle es un caso particular del teorema del valor medio, en el que f(a) = f(b).
Teorema fundamental del Calculo
consiste (intuitivamente) en la afirmación de que la derivación e integración de una función son operaciones inversas. Esto significa que toda función continua integrable verifica que la derivada de su integral es igual a ella misma. Este teorema es central en la rama de las matemáticas denominada análisis matemático o cálculo.
El teorema es fundamental porque hasta entonces el cálculo aproximado de áreas -integrales- en el que se venía trabajando desde Arquímedes, era una rama de las matemáticas que se seguía por separado al cálculo diferencial que se venía desarrollando por Isaac Newton, Isaac Barrow y Gottfried Leibniz en el siglo XVIII y dio lugar a conceptos como el de las derivadas. Las integrales eran investigadas como formas de estudiar áreas y volúmenes, hasta que en ese punto de la historia ambas ramas convergieron, al demostrarse que el estudio del "área bajo una función" estaba íntimamente vinculado al cálculo diferencial, resultando la integración, la operación inversa a la derivación.
Una consecuencia directa de este teorema es la regla de Barrow, denominada en ocasiones segundo teorema fundamental del cálculo, y que permite calcular la integral de una función utilizando la integral indefinida de la función al ser integrada.
El teorema es fundamental porque hasta entonces el cálculo aproximado de áreas -integrales- en el que se venía trabajando desde Arquímedes, era una rama de las matemáticas que se seguía por separado al cálculo diferencial que se venía desarrollando por Isaac Newton, Isaac Barrow y Gottfried Leibniz en el siglo XVIII y dio lugar a conceptos como el de las derivadas. Las integrales eran investigadas como formas de estudiar áreas y volúmenes, hasta que en ese punto de la historia ambas ramas convergieron, al demostrarse que el estudio del "área bajo una función" estaba íntimamente vinculado al cálculo diferencial, resultando la integración, la operación inversa a la derivación.
Una consecuencia directa de este teorema es la regla de Barrow, denominada en ocasiones segundo teorema fundamental del cálculo, y que permite calcular la integral de una función utilizando la integral indefinida de la función al ser integrada.
Sumas de RIEMANN
es un método de integración numérica que nos sirve para calcular el valor de una integral definida es decir el área bajo una curva, este metodo es muy útil cuando no es posible utilizar el Teorema Fundamental del Cálculo. Estas sumas toman su nombre del matemático alemán Bernhard Riemann.
La suma de Riemann consiste básicamente en trazar un número finito de rectangulos dentro de un área irregular, calcular el área de cada uno de los rectangulos y sumarlos. El problema de este método de integración numérica es que al sumar las áreas se obtiene un margen de error muy grande.
La suma de Riemann consiste básicamente en trazar un número finito de rectangulos dentro de un área irregular, calcular el área de cada uno de los rectangulos y sumarlos. El problema de este método de integración numérica es que al sumar las áreas se obtiene un margen de error muy grande.
sábado, 10 de diciembre de 2011
Productos Notables
Sabemos que se llama producto al resultado de una multiplicación. También sabemos que los valores que se multiplican se llaman factores.
Se llama productos notables a ciertas expresiones algebraicas que se encuentran frecuentemente y que es preciso saber factorizarlas a simple vista; es decir, sin necesidad de hacerlo paso por paso.
Se les llama productos notables (también productos especiales) precisamente porque son muy utilizados en los ejercicios.
A continuación veremos algunas expresiones algebraicas y del lado derecho de la igualdad se muestra la forma de factorizarlas (mostrada como un producto notable).
Cuadrado de la suma de dos cantidades o binomio cuadrado
a2 + 2ab + b2 = (a + b)2
Cuadrado de la diferencia de dos cantidades
El cuadrado de la diferencia de dos cantidades es igual al cuadrado de la primera cantidad, menos el doble de la primera cantidad multiplicada por la segunda, más el cuadrado de la segunda cantidad.
Demostración:
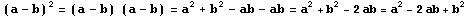
Producto de la suma por la diferencia de dos cantidades (o producto de dos binomios conjugados)
Cubo de una suma
Cubo de una diferencia
Se llama productos notables a ciertas expresiones algebraicas que se encuentran frecuentemente y que es preciso saber factorizarlas a simple vista; es decir, sin necesidad de hacerlo paso por paso.
Se les llama productos notables (también productos especiales) precisamente porque son muy utilizados en los ejercicios.
A continuación veremos algunas expresiones algebraicas y del lado derecho de la igualdad se muestra la forma de factorizarlas (mostrada como un producto notable).
Cuadrado de la suma de dos cantidades o binomio cuadrado
a2 + 2ab + b2 = (a + b)2
Cuadrado de la diferencia de dos cantidades
a2 – 2ab + b2 = (a – b)2 |
El cuadrado de la diferencia de dos cantidades es igual al cuadrado de la primera cantidad, menos el doble de la primera cantidad multiplicada por la segunda, más el cuadrado de la segunda cantidad.
Demostración:
Producto de la suma por la diferencia de dos cantidades (o producto de dos binomios conjugados)
(a + b) (a – b) = a2 – b2 |
Cubo de una suma
a3 + 3a2b + 3ab2 + b3 = (a + b)3 |
Cubo de una diferencia
a3 – 3a2b + 3ab2 – b3 = (a – b)3 |
Identidades pitagoricas
Es una igualdad entre expresiones que contienen funciones trigonométricas y es válida para todos los valores del ángulo en los que están definidas las funciones (y las operaciones aritméticas involucradas).
Notación: se define cos2α, sen2α, otros; tales que sen2α es (sen α)2.
Notación: se define cos2α, sen2α, otros; tales que sen2α es (sen α)2.
| Relación pitagórica |  |
|---|---|
| Identidad de la razón | 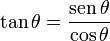 |
|---|
Funciones Trigonometricas
son las funciones que se definen a fin de extender la definición de las razones trigonométricas a todos los números reales.
Las funciones trigonométricas son de gran importancia en física, astronomía, cartografía, náutica, telecomunicaciones, la representación de fenómenos periódicos, y otras muchas aplicaciones.
Las Razones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo asociado a sus ángulos. Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circunferencia unitaria (de radio unidad). Definiciones más modernas las describen como series infinitas o como la solución de ciertas ecuaciones diferenciales, permitiendo su extensión a valores positivos y negativos, e incluso a números complejos.
Existen seis funciones trigonométricas básicas. Las últimas cuatro, se definen en relación de las dos primeras funciones, aunque se pueden definir geométricamente o por medio de sus relaciones. Algunas funciones fueron comunes antiguamente, y aparecen en las primeras tablas, pero no se utilizan actualmente; por ejemplo el verseno (1 − cos θ) y la exsecante (sec θ − 1).
Las funciones trigonométricas son de gran importancia en física, astronomía, cartografía, náutica, telecomunicaciones, la representación de fenómenos periódicos, y otras muchas aplicaciones.
Las Razones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo asociado a sus ángulos. Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circunferencia unitaria (de radio unidad). Definiciones más modernas las describen como series infinitas o como la solución de ciertas ecuaciones diferenciales, permitiendo su extensión a valores positivos y negativos, e incluso a números complejos.
Existen seis funciones trigonométricas básicas. Las últimas cuatro, se definen en relación de las dos primeras funciones, aunque se pueden definir geométricamente o por medio de sus relaciones. Algunas funciones fueron comunes antiguamente, y aparecen en las primeras tablas, pero no se utilizan actualmente; por ejemplo el verseno (1 − cos θ) y la exsecante (sec θ − 1).
| Función | Abreviatura | Equivalencias (en radianes) |
|---|---|---|
| Seno | sin (sen) |  |
| Coseno | cos |  |
| Tangente | tan |  |
| Cotangente | ctg (cot) |  |
| Secante | sec |  |
| Cosecante | csc (cosec) |  |
Suscribirse a:
Comentarios (Atom)
